- 大学で勉強した基本的な知識はもう忘れてしまった
- 過去問を解くために最低限必要な知識を勉強したい
- 過去問を解くときのおすすめ参考書を知りたい
技術士一次試験の基礎科目では、科学技術に関する全般的な基礎知識があるかどうかが見られます。
しかし、全般的な基礎知識は大学で学んだきり、今ではもうすっかり忘れてしまったという方は多いのではないでしょうか?
そこで、本記事では基礎科目を解くために最低限必要な知識をわかりやすく解説しました。
この記事を読んでから過去問を繰り返し解くことで、ひとまず合格基準である正答率50%を超えることが出来るはずです。
本記事では無駄に多くを解説せず、必要な分だけ知識をまとめています。
比較的読みやすいボリュームになっていますので、読んでみてくださいね。
技術士一次試験全般の対策方法についてはこちら
⇒技術士一次試験の概要と試験対策【技術士の道しるべ】
技術士一次試験 基礎科目の概要
基礎科目では科学技術全般にわたる基礎知識を問われます。
出題内容は、4年制大学の自然科学系学部の専門教育課程修了程度です。
次の問題群から、それぞれ6問、計30問出題され、各問題群からそれぞれ3問ずつを選択して計15問を解答します。
- (1群) 設計・計画に関するもの〔 設計理論、システム設計、品質管理等 〕
- (2群) 情報・論理に関するもの〔 アルゴリズム、情報ネットワーク等 〕
- (3群) 解析に関するもの〔 力学、電磁気学等 〕
- (4群) 材料・化学・バイオに関するもの〔 材料特性、バイオテクノロジー等 〕
- (5群) 環境・エネルギー・技術に関するもの〔 環境、エネルギー、技術史等 〕
合格基準は8問以上正解となっています。
一次試験は全てマークシート方式(5肢択一式)となっています。
各問題で正解か不正解かがはっきり分かれますので、合格か不合格かもはっきりとわかります。
それでは、技術士一次試験の基礎科目に合格するために最低限必要な知識を解説していきます。
(1群) 設計・計画に関するもの
システムの信頼性
システム信頼性は「あるシステムが正常に動作する確率」を求める問題です。
例えば、下図のようにA,B,Cという部品の組み合わせで構成されているシステムの信頼性を考えます。部品A、部品B、部品Cが正常に動作する信頼性はそれぞれ0.9(90%)とします。
この場合、部品をそのまま直列につないだ場合と並列につないだ場合の信頼性は以下のようになります。
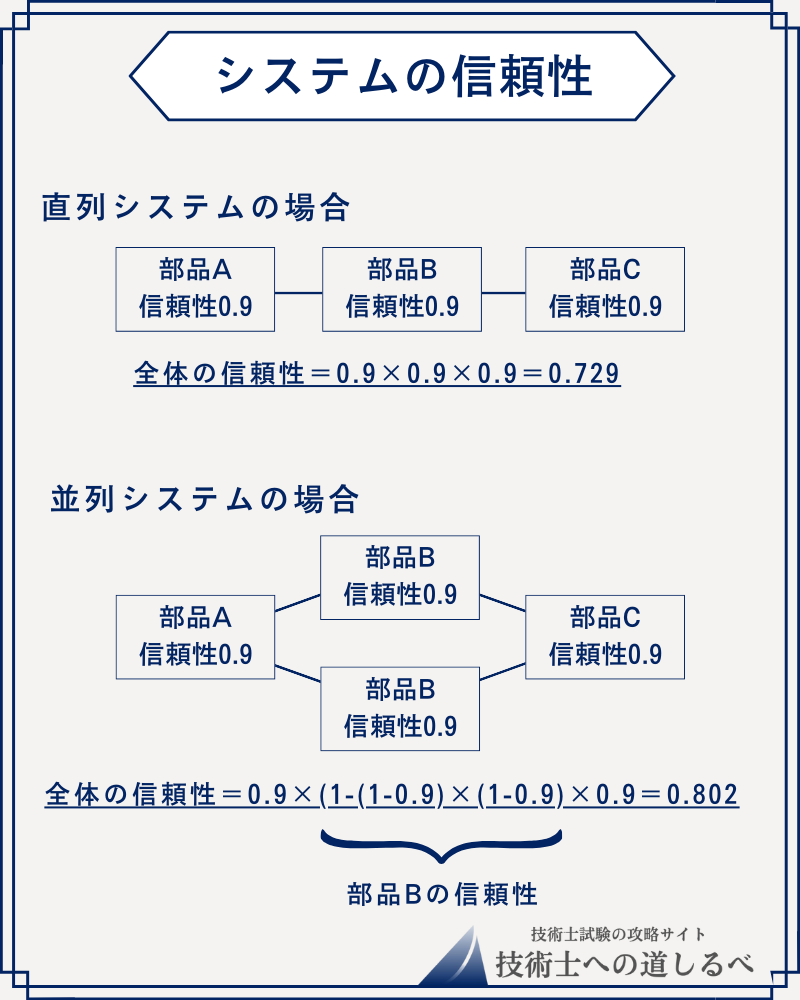

並列にすると信頼性が向上していますよね。
このように部品を並列に繋ぐことを冗長化と言います。
システムの信頼性に関する問題は高い確率で出題されます。
出題パターンは様々でぱっと見は難しく見えますが、ポイントさえ抑えておけば簡単に解ける問題ばかりですのでしっかり理解しましょう。
下図に示した、互いに独立な3個の要素が接続されたシステムA〜Eを考える。
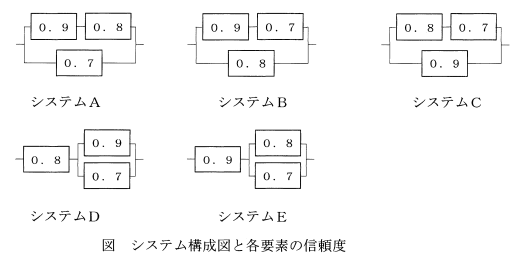
3個の要素の信頼度はそれぞれ0.9, 0.8, 0.7 である。各システムを信頼度が高い順に並べたものとして、最も適切なものはどれか。
1 .C > B > E > A > D
2 .C > B > A > E > D
3 .C > E > B > D > A
4 .E > D > A > B > C
5 .E > D > C > B > A
答え:2
地道に計算していきましょう。
Aの信頼度:(上部)0.9×0.8=0.72、(全体)1-(1-0.72)(1-0.7)=0.916
Bの信頼度:(上部)0.9×0.7=0.63、(全体)1-(1-0.63)(1-0.8)=0.926
Cの信頼度:(上部)0.8×0.7=0.56、(全体)1-(1-0.56)(1-0.9)=0.956
Dの信頼度:(右部)1-(1-0.9)(1-0.7)=0.97、(全体)0.8×0.97=0.776
Eの信頼度:(右部)1-(1-0.8)(1-0.7)=0.94、(全体)0.9×0.94=0.846
以上より、「2」が正解となります。
引用:技術士第一次試験 令和3年度(2021年) 基礎科目「設計・計画に関するもの」問2
待ち行列(オペレーションズリサーチ)
待ち行列は「ある行列に並んだ時の平均の待ち時間」を求める問題です。
例えば、下図のようにお客さんが並んでいるスーパーのレジの待ち時間を考えます。この時の待ち時間は「レジが1時間あたり何人処理できるか」「行列に1時間あたり何人並ぶか」さえ分かれば以下のように計算できます。
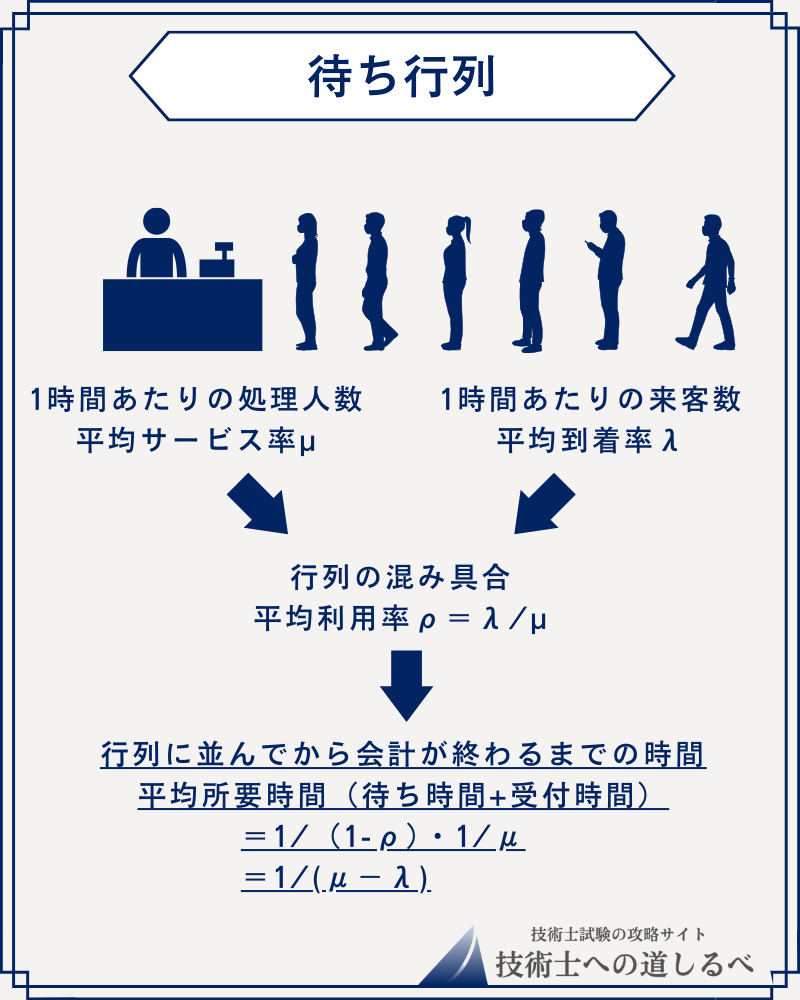

試験本番では公式が与えられているケースが多いので、
公式を丸暗記する必要はないでしょう。
余談ですが、公式は以下のようにイメージすると覚えやすいかもしれません。
・来客数である「λ」はテクテクと人が歩いているイメージ
・処理人数である「µ」はレジでバーコードをピッと読み取る機械のイメージ
ある銀行に1台のATMがあり、このATMを利用するために到着する利用者の数は1時間当たり平均40人のポアソン分布に従う。また、このATMでの1人当たりの処理に要する時間は平均40秒の指数分布に従う。このとき、利用者がATMに並んでから処理が終了するまで系内に滞在する時間の平均値として最も近い値はどれか。
トラフィック密度(利用率)= 到着率 ÷ サービス率
平均系内列長 = トラフィック密度 ÷(1 – トラフィック密度)
平均系内滞在時間 = 平均系內列長 ÷ 到着率
1 .68秒
2 .72秒
3 .85秒
4 .90秒
5 .100秒
答え:2
与えられた条件をもとに地道に計算していきましょう。
「到着する利用者の数は1時間当たり平均40人」ということは平均到着率=40[人/時間]。
「1人当たりの処理に要する時間は平均40秒」ということは平均サービス率=90[人/時間]。
あとは公式に当てはめるだけです。
トラフィック密度=40/90
平均系内列長=40/90÷(1-40/90)=0.8
平均系内滞在時間=0.8÷40=0.02[時間]=72[秒]
以上より、「2」の72秒が正解になります。
引用:技術士第一次試験 令和元年度(2019年) 基礎科目「設計・計画に関するもの」 問5
ユニバーサルデザイン
ユニバーサルデザインとは「出来るだけ多くの人が使いやすいように製品・建物・環境をデザインする」という考え方です。
ユニバーサルデザインには7つの原則がありますので、これは覚えておくと良いでしょう。
- 誰でも使える公平性
- 使い方が選べる柔軟性
- 直感的で簡単に使える単純性
- 必要な情報がすぐに分かる明確さ
- 使い方をミスしても危険につながらない安全性
- 無理なく使える身体への負担の少なさ
- 使いやすい大きさや広さであるという空間性
次のうち、ユニバーサルデザインの特性を備えた製品に関する記述として、最も不適切なものはどれか。
1 .小売店の入り口のドアを、ショッピングカートやベビーカーを押していて手がふさがっている人でも通りやすいよう、自動ドアにした。
2 .録音再生機器(オーディオプレーヤーなど)に、利用者がゆっくり聴きたい場合や速度を速めて聴きたい場合に対応できるよう、再生速度が変えられる機能を付けた。
3 .駅構内の施設を案内する表示に、視覚的な複雑さを軽減し素早く効果的に情報が伝えられるよう、ピクトグラム(図記号)を付けた。
4 .冷蔵庫の扉の取っ手を、子どもがいたずらしないよう、扉の上の方に付けた。
5 .電子機器の取扱説明書を、個々の利用者の能力や好みに合うよう、大きな文字で印刷したり、点字や音声・映像で提供したりした。
答え:4
4は子供が使用出来なくなるデザインのため、ユニバーサルデザインとはいえません。
このデザイン自体は安全性が高まる効果があり悪いものではありません。ただ、「誰にでも使える」というユニバーサルデザインの主旨とは異なるということですね。
引用:技術士第一次試験 令和3年度(2021年) 基礎科目「設計・計画に関するもの」 問1
(2群) 情報・論理に関するもの
2進数
私たちが普段よく使っている数字は10進数です。
10進数は「0」から「9」までの10種類の数字を使って数を表現しています。「0」から数えて「9」までいき、その次は「10」というように桁があがる表現方法です。
一方、コンピュータの世界では2進数が使われています。
2進数とは、「0」と「1」の2種類の数字を使って数を表現しています。2進数では「0」「1」と数えたら、その次は「10」というように桁があがる表現方法です。
この2進数に関連する問題は良く出題されますので、2進数の基礎を理解しておきましょう。
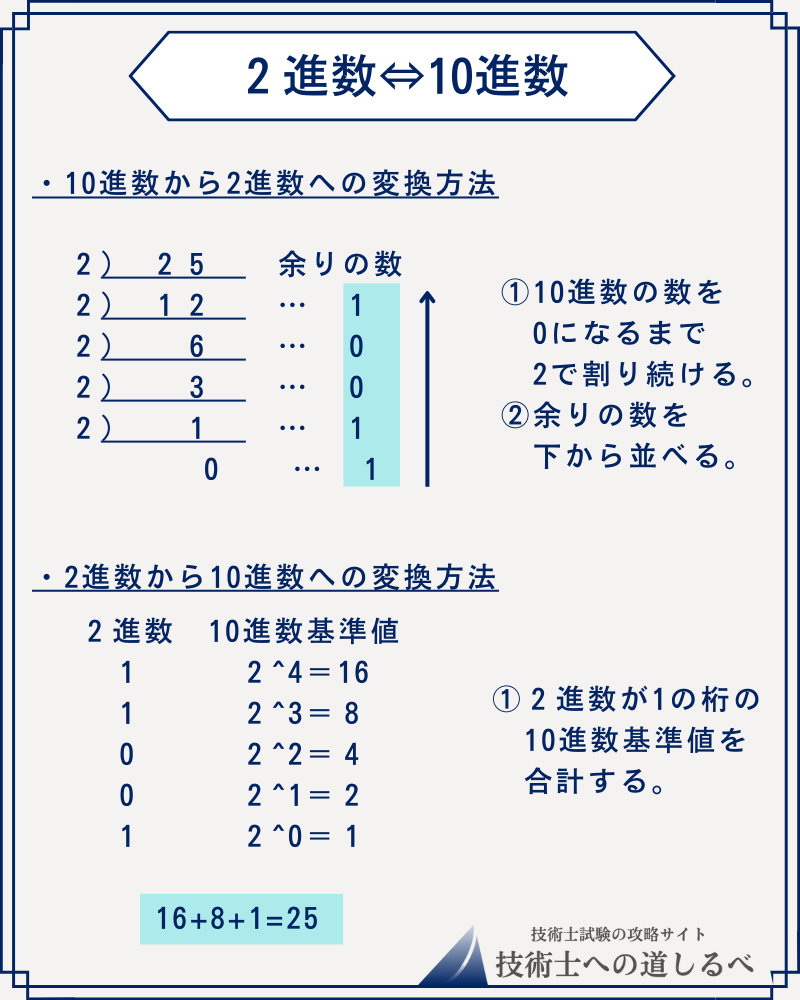
10進数での「10分の1」を2進表現したものとして最も適切なものはどれか。ただし、以下の2進表現では、小数点以下16位までを示している。
1 0.0000011001100110
2 0.0000110011001100
3 0.0001100110011001
4 0.0011001100110011
5 0.0110011001100110
答え:3
10進数から2進数への変換の応用ですね。
10進数の少数を2進数に変換する際は次のように行います。
①10進数の小数の部分が0になるまで、小数の部分に2をかけ続ける。
②求めた積の整数の部分を上から並べる。
例えば、10進数の「0.1」を2進数に変換する場合は以下のようになります。
0.1 × 2 = 0.2 → 0
0.2 × 2 = 0.4 → 0
0.4 × 2 = 0.8 → 0
0.8 × 2 = 1.6 → 1
0.6 × 2 = 1.2 → 1
0.2 × 2 = 0.4 → 0
0.4 × 2 = 0.8 → 0
0.8 × 2 = 1.6 → 1
0.6 × 2 = 1.2 → 1
(以下ループ)
このように、10進数の「0.1」を2進数に変換すると「0.000110011…」となります。
以上より、「3」の0.0001100110011001が正解となります。
引用:技術士第一次試験 平成27年度(2015年) 基礎科目「情報・論理に関するもの」 問9
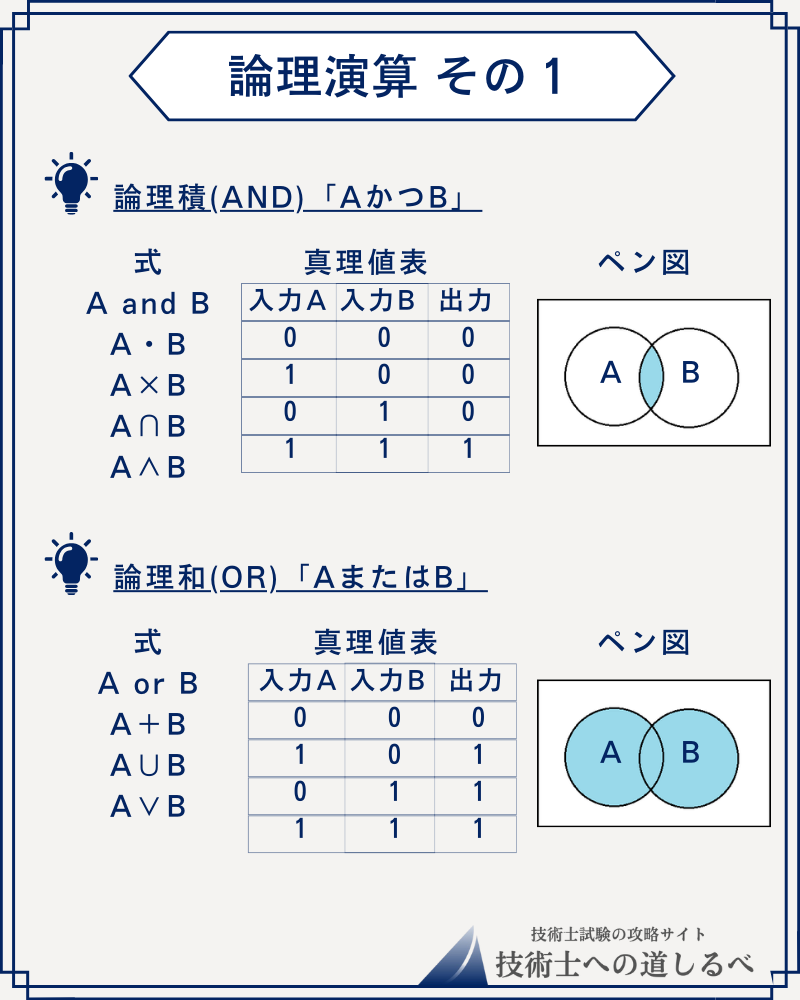
論理演算(ペン図)
論理演算とは、真(true)か偽(false)かのふたつの値だけを用いて結果を表す演算方法です。
代表的な論理演算として
「論理積(AND)」
「論理和(OR)」
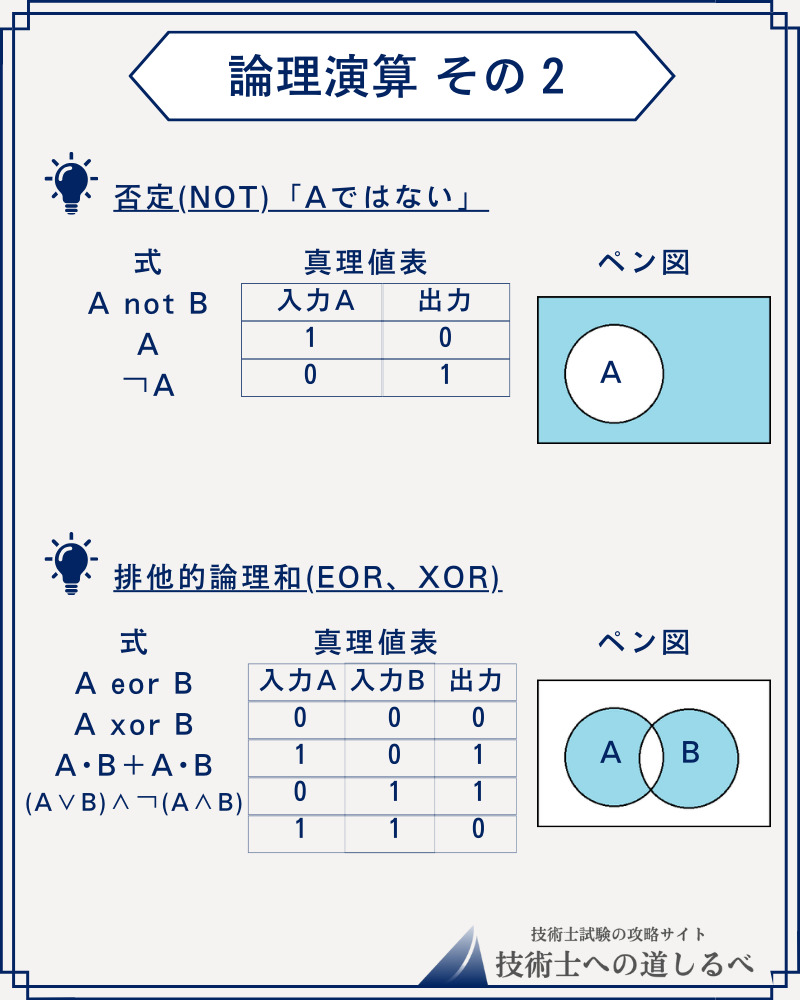
「否定(NOT)」
「排他的論理和(XOR)」
があります。この4つは覚えておきましょう。
ある村に住民A,B、C,Dの4名が住んでいる。ここでは、重要なことがらの決定には全員が会議に出席して決めることになっているが、以下のように、他人の意見を見ながら自分の意見を決める住民がいる。
※住民Cは、住民AとBが共に議案に賛成のときに反対し、それ以外のときは議案に賛成する。
※住民Dは、住民AとCが共に議案に賛成のときに反対し、それ以外のときは議案に賛成する。
このとき、次の記述のうち最も適切なものはどれか。なお、住民は、必ず賛成か反対のどちらかの決定をするものとする。
1 住民Cが議案に賛成するのは、住民Aと住民Bが共に賛成するときだけである。
2 住民Cが議案に賛成するのは、住民Aと住民Bの賛否が異なるときだけである。
3 住民Dが議案に賛成するのは、住民Aと住民Bが共に賛成するときだけである。
4 住民Dが議案に賛成するのは、住民Aと住民Bの賛否が異なるときだけである。
5 住民Bが議案に賛成すれば、必ず住民Dも議案に賛成する。
答え:5
なんだかクイズのようですが、論理式の問題です。
ひとつずつ確認して、適切なものがどれかを選びましょう。
引用:技術士第一次試験 平成27年度(2015年) 基礎科目「情報・論理に関するもの」 問8
(3群) 解析に関するもの
材料力学
材料力学とは、機械や構造物などを構成する材料に荷重が加わった時に材料がどのように変形・破壊するかを研究する学問です。
力学という分野には材料力学以外にも熱力学や流体力学などがありますが、技術士一次試験では特に材料力学に関する問題がよく出題されます。
材料力学自体は一朝一夕で身につくものではありませんが、技術士一次試験で出題される程度ならこれから解説する知識でひと通り解けるようにはなるはずです。
※もちろん、過去問を解いてトレーニングする必要はあります。
応力
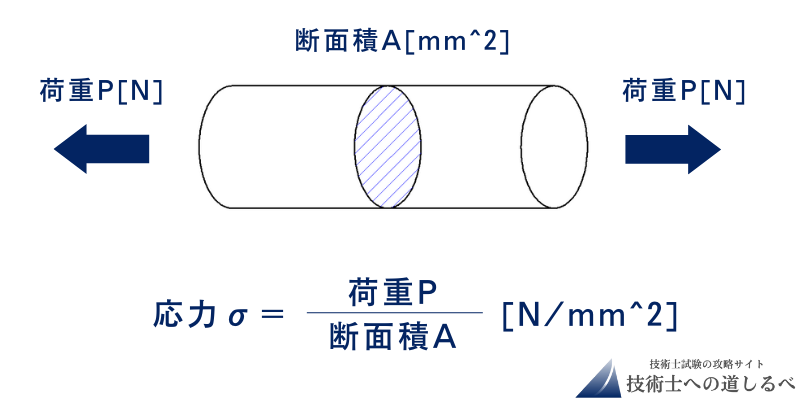
「応力」とは、材料内部に発生してする単位面積あたりの力のことです。
例えば、丸棒を引っ張った時にはそれに反発するように元の形に戻そうとする力が発生します。この反発している力を断面積で割った値が「応力」となります。
引っ張る力をP [N]、断面積をA [mm2]とした時、応力は以下の式で表せます。
応力σ=引っ張る力P/断面積A [N/mm2]
ひずみ
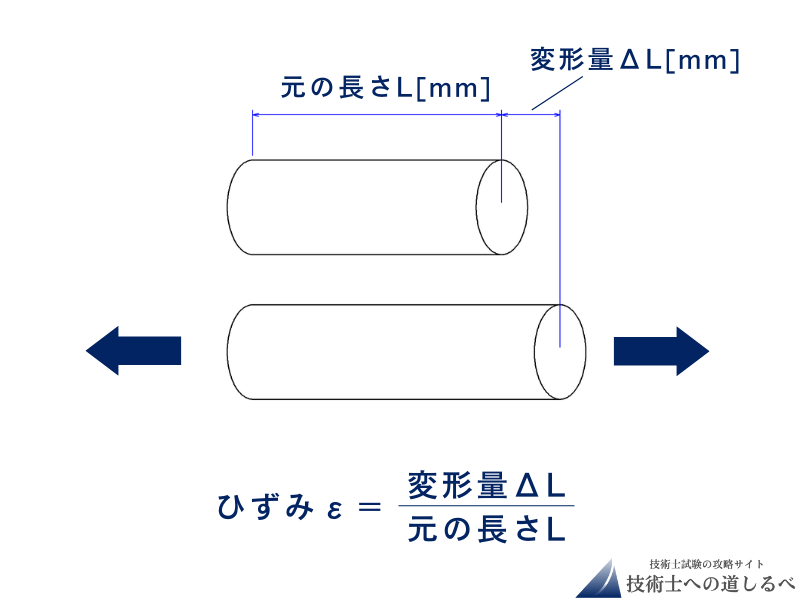
材料を引っ張ったり押したりして荷重を加えると、材料は多かれ少なかれ変形します。この時、材料が変形した割合を「ひずみ」といいます。
元の長さをL [mm]、変形量をΔL [mm]とした時、ひずみは以下の式で表せます。
ひずみε=変形量ΔL/元の長さL (単位なし)
ヤング率(縦弾性係数)
ヤング率は材料の「変形しにくさ」を表す特性値です。
ヤング率は材料固有の特性値です。
ヤング率は以下の式で定義されます。
ヤング率E=応力σ/ひずみε
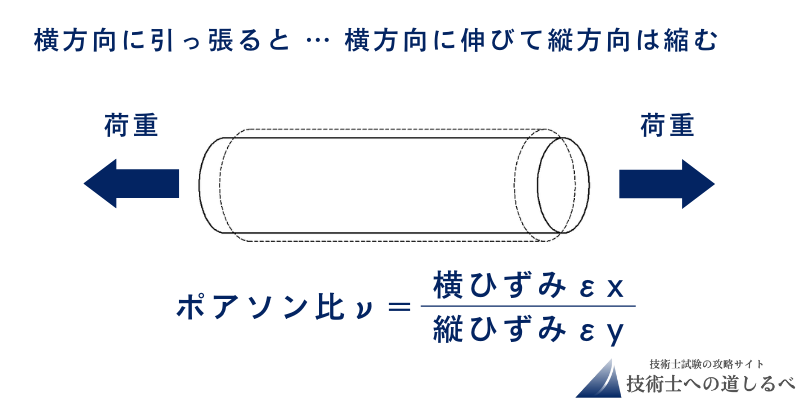
ポアソン比
物体に荷重を加えると縦と横方向にひずみますが、この縦と横のひずみ(歪み)の比のことをポアソン比といいます。
ポアソン比も材料固有の特性値です。
例えば、棒を引張ると引っ張った方向に棒は伸び、垂直方向は逆に細くなります。この伸びる現象を縦ひずみ、細くなる現象を横ひずみといい、ポアソン比は「横ひずみ/縦ひずみ」で求められます。
ポアソン比ν=横ひずみεx/縦ひずみεy
下図に示すように、同じ長さLの棒A( 断面積AA、縦弾性係数( ヤング係数EA ) )と棒B( 断面積AB、縦弾性係数( ヤング係数 )EB)の両端が剛板に接着され、そこに引張力Pが作用している。棒Aと棒Bには、同じ長さの伸びが生じる。このとき、棒Aと棒Bに生じている引張応力σAとσBの比として、最も適切なものはどれか。

答え:4
ヤング率の公式を使って解いていきましょう。
問題文より、棒Aと棒Bのひずみは同じと読み取れますね。
よって、ヤング率の公式から ε=σA/EA=σB/EB となり、
これを変形すると σA/σB=EA/EB となります。
以上より、正解は4となります。
引用:技術士第一次試験 平成28年度(2016年) 基礎科目「解析に関するもの」 問18
(4群) 材料・化学・バイオに関するもの
準備中
(5群) 環境・エネルギー・技術に関するもの
科学技術の偉業者
ガリレオやアインシュタインなど、科学技術の偉業者に関する問題です。
誰が出てくるかはランダムですが、この問題はほぼ毎年出題されています。
暗記物ですので、覚えてしまえば得点源にしやすい問題です。
きっちりと覚えていきましょう。
平成26年度以降出題された偉業者達をまとめておきました。
これを覚えておけばほぼ問題ないでしょう。
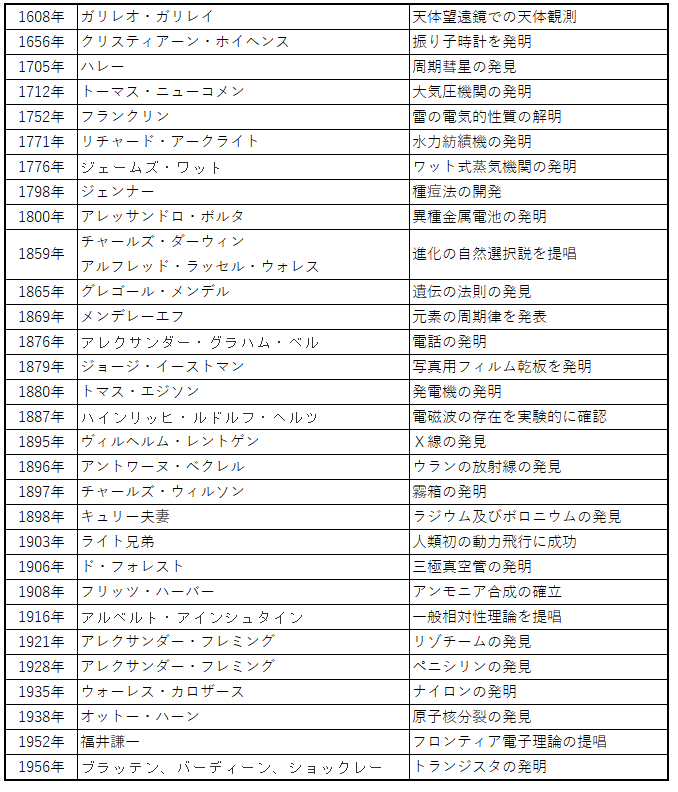
次の(ア)〜(オ)の、社会に大きな影響を与えた科学技術の成果を、年代の古い順から並べたものとして、最も適切なものはどれか。
(ア)フリッツ・ハーバーによるアンモニアの工業的合成の基礎の確立
(イ)オットー・ハーンによる原子核分裂の発見
(ウ)アレクサンダー・グラハム・ベルによる電話の発明
(エ)ハインリッヒ・ルドルフ・ヘルツによる電磁波の存在の実験的な確認
(オ)ジェームズ・ワットによる蒸気機関の改良
① ア → オ → ウ → エ → イ
② ウ → エ → オ → イ → ア
③ ウ → オ → ア → エ → イ
④ オ → ウ → エ → ア → イ
⑤ オ → エ → ウ → イ → ア
答え:4
年代通りに並べ替えれば解答できます。
引用:技術士第一次試験 令和3年度(2021年) 基礎科目「環境・エネルギー・技術に関するもの」 問29
過去問を解こうおすすめテキスト
必要な知識を確認したら、次は実際に過去問を解いてみましょう。
過去問はこちらのページから参照できます。
⇒過去問題(第一次試験)|公益社団法人 日本技術士会 (engineer.or.jp)
技術士会ホームページに過去問の正答は載っていますが、解説は全くないので注意してください。
分からない問題があればこのページやネットで検索して勉強をしていく必要があります。
「ネットで検索して個別に勉強する」というのは結構時間が掛かります。
そこまでの時間がとれないという方は参考書を使って過去問を解くことをおすすめします。
技術士試験に特化した参考書なら過去問の解説が掲載されていますので、ネットで検索して勉強するという必要もありません。
参考書一冊で試験勉強を完結することができます。

最小の労力で技術士一次試験に合格したいという方にはおすすめです
こちらの参考書なら解説付きですし、適性科目もまとめて対策できてコスパが良いためおすすめです。
一次試験用の参考書はこちらの記事でおすすめのものを紹介していますので参考にしてみてください。
⇒【独学向け】技術士一次対策おすすめ参考書3選+α【技術士が選ぶ】
まとめ
技術士一次試験 基礎科目について知っておくべき基礎的な知識を解説しました。
この記事で基礎的な知識を確認しておき、さらに過去問を解くことで合格基準を満たせる実力がつくはずです。
繰り返し過去問を解いて、ぜひ技術士一次試験に合格してください。





コメント